In lectures at NMSS, we certainly learn new maths. But we also learn a bit about some of the great men and women of mathematics. One such person is Archimedes. Archimedes lived in the third century BC in the city of Syracuse, in Ancient Greece.
Archimedes
(http://www.ballonflug.org/archimedes.htm. Licensed under Public Domain via Wikimedia Commons)
Today, he is most famous for supposedly running naked through the streets of Syracuse shouting “Eureka!” after he figured out a way to precisely measure volumes of irregular objects using displacement of water.
Eureka!
However, during his lifetime, Archimedes made significant contributions to mathematics and to engineering. He also made many useful inventions. One of these, the Archimedes screw is still used today in developing countries for raising water. He calculated very accurate values for several irrational numbers. He understood the concept of infinity and pre-empted calculus. He developed an understanding of the mathematical behaviour of levers, pulleys and fulcrums, and worked out how to calculate the surface areas and volumes of cylinders and spheres.
In fact, Archimedes’ contribution to mathematics was deemed so significant that his face appears on the Fields Medal (which is like the Nobel Prize, but for mathematics).
Front side of the Fields Medal. Designed by Stefan Zachow
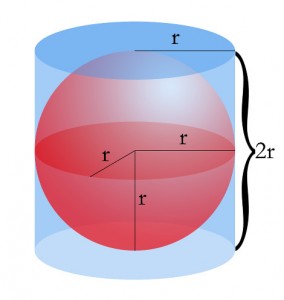
Of all Archimedes’ work, he believed that the best thing he ever did was to figure out that the volume of a sphere is two thirds the volume of a circumscribed cylinder.
A sphere inscribed within a cylinder
Image by Andertxuman. Licenced under Public Domain via Wikimedia Commons
He expressed it this way:
“Any sphere is (in respect of solid content) four times the cone with base equal to a great circle of the sphere and height equal to its radius; and the cylinder with base equal to a great circle of the sphere and height equal to the diameter is 1½ times the sphere.”
Archimedes liked this so much that he asked to have a picture of a cylinder circumscribing a sphere put on his tombstone.
I was first introduced to his ingenious and beautiful technique of computing the volume of a sphere during a lecture at NMSS. In part 2 of this post I show you a version of it. The amazing thing about this method is that you don’t need any advanced mathematics to work it out, only some geometry and a knowledge of fulcrums.
This work by Archimedes appears in a treatise, called The Method of Mechanical Theorems, that forms a letter to Eratosthenes (in maths, Eratosthenes is still known because he came up with the “sieve of Eratosthenes”, which is a way to find prime numbers). Until the 20th century, The Method of Mechanical Theorems was thought to have been lost forever. However, one copy of it is now known to exist. It is called the Archimedes Palimpsest. It was first found in Constantinople in 1906 by the Danish professor Johan Heiberg who discovered that a 13th century Byzantine prayer book had been written over the top of a number of ancient manuscripts, one of which was The Method of Mechanical Theorems. The Archimedes Palimpsest then disappeared until 1998 when it arrived at the Walters Art Museum in Baltimore, where a team has been working to recover all of the original manuscripts. All of the original images and transcripts have been placed on the Internet, so you can see them for yourself. The Method of Mechanical Theorems has also been translated into English by T. Heath under the title The Method of Archimedes (Cambridge University Press, 1912). This work is also available on the Internet, so you can read the original for yourself; a very interesting exercise.
